the random walk

RRN
2017-01-21
research

The Random Walk

“A line is a dot that went for a walk.” – Paul Klee

Random walk models are stochastic models that describe how individual members of a population (of agents) arrive at their respective locations, which then in turn contribute and add up to an overall state of aggregate distribution. The simple random walk is often considered the most simple concept of movement in an agent- based simulation. Individual steps in such a movement are strictly independent of one another, a random walk’s trajectory is determined entirely by random effects and by its own previous evolution, rather than by an agent’s environment or other agents’ behavior.

For a random walk imagine a two dimensional plane with a Cartesian grid and an agent initially located at its origin (0/0). The agent’s walk is composed of a series of subsequent steps of unit length in any direction. The plane angle selected in each iteration is entirely random, with no connection between the direction of the previous step and the current one. The most generic NetLogo code generating a random walk would then probably read somehow like this:

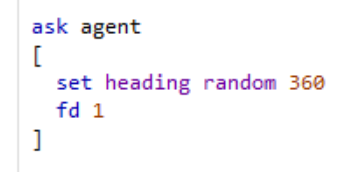
And generate this kind of output:

While it is quite safe to assume that not many moving entities in nature move completely at random, it is still sensible to use random walks as a conceptual starting point for further refinements in order to understand more complex behavioral patterns of movement and their underlying logic.

In any office environment a movement path, which is determined by randomness alone, is not a plausible option. A more realistic and life-like agent model in its generic form needs to incorporate basic movement constraints such as step correlation (“purposeful” walk) or wall and boundary detection and include behavioral concepts such collision avoidance (with both, other agents and objects in the scene) and zone detection. For these further explorations the random walk will serve as a null model to build up upon and to compare spatial patterns against.